10:10
[익명]
수학 문제 알려주세요ㅠ 이거 어케 푸나용
이거 어케 푸나용
## 0655번 문제 풀이
문제: 이차함수 y = -3x² + 18x + k - 7 의 최댓값이 6일 때, 상수 k의 값은?
### 1. 이차함수의 표준형 변환 과정
최댓값을 찾기 위해 일반형 식을 완전제곱식 꼴로 고칩니다.
1.x²의 계수인 -3으로 x가 포함된 항을 묶습니다. y = -3(x² - 6x) + k - 7
2.괄호 안을 완전제곱식으로 만들기 위해 x 계수(-6)의 절반의 제곱인 9를 더하고 뺍니다.
y = -3(x² - 6x + 9 - 9) + k - 7
3.괄호 밖으로 -9를 내보낼 때 앞의 계수 -3과 곱해져서 나갑니다.
(-3 × -9 = +27)
y = -3(x - 3)² + 27 + k - 7
4.식을 정리합니다. y = -3(x - 3)² + k + 20
### 2. 최댓값을 이용한 k값 계산
이 함수는 x²의 계수가 음수(-3)이므로 위로 볼록한 포물선이며, 꼭짓점에서 최댓값을 가집니다.
●꼭짓점의 좌표: (3, k + 20)
●최댓값: k + 20
문제에서 최댓값이 6이라고 했으므로 식을 세우면: k + 20 = 6
따라서 k의 값은 다음과 같습니다. k = 6 - 20 k = -14
정답: ① -14
### 검토 내용
●부호 확인: 표준형 변환 과정에서 +27과 -7을 더해 +20이 되는 과정이 정확합니다.
●최종 답안: k = -14일 때 최댓값 6이 성립함을 확인했습니다.
회원가입 혹은 광고 [X]를 누르면 내용이 보입니다
-
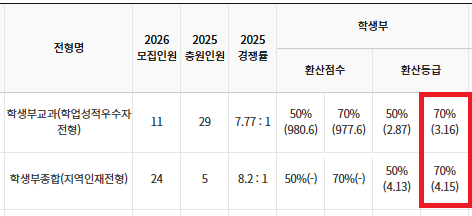
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -

아이폰 16, 16프로 케이스 호환 가능한가요? 16을 쓰고 있는데 일반형은 케이스가 많이 없고 프로형은 많아서
2025.12.01 -

임영웅 11월 브랜드평판 순위 알고싶어요 임영웅 11월 브랜드평판에서 스타부문에서의 임영웅 순위 알고싶어요
2025.11.30 -

전주 고등학교 다자녀 제가 2027학년도 고등학교 입학생인데요 지망하는 학교가 전주 한일고인데 1. 다자녀
2025.11.30 -
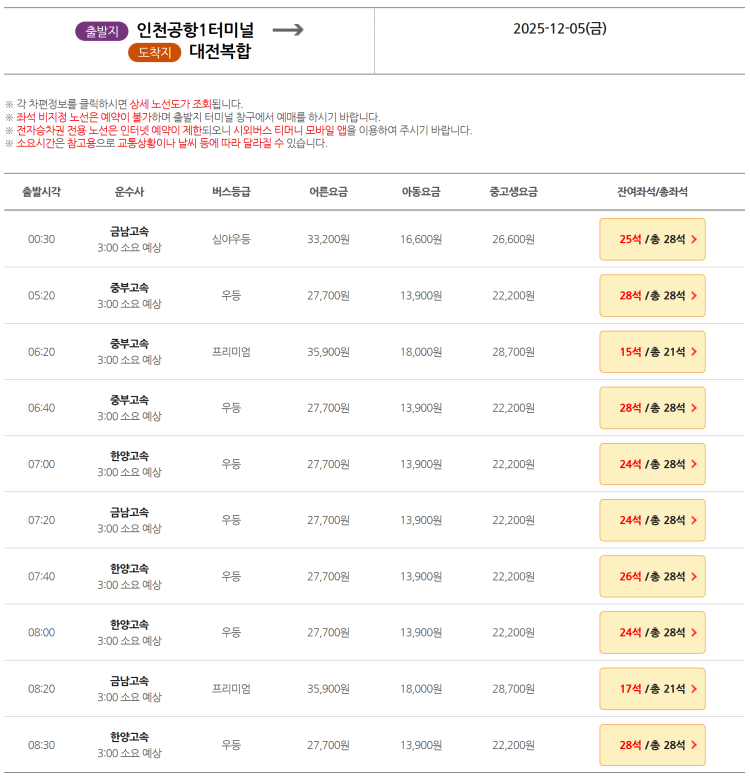
고속버스 예매 인천공항에서 대전으로 가는 버스를 이용하려하는데 버스 노선이 인천공항 2터미널에서 출발해
2025.11.30 -

어떤 야구선수 싸인일까요? 제가 옛날에 롯데 자이언츠 선수한테 싸인받은 싸인볼을 오늘 찾았네요. 어떤
2025.11.29
